Finding Latent Faces-with Non-negative Matrix Factorization

Non-negative matrix factorization is a fast technique for generating embeddings from a dataset. More concretely, given a matrix you can decompose it into two matrices that are approximattely multiplicands of the matrix. I.e. given matrix M, it finds matrices A and B such that M ≈ AB.

A very cool thing about embedding matrices is that the rows and columns that comprise these matrices naturally tend to fill with values that will multiply together to create the values in your data. More concretely again, if your dataset is pictures of faces, and embedding matrix will be composed of face-like images that will be added together in varying amounts to make the faces in the dataset.

So let’s make some faces.

Thankfully sklearn.decomposition has an NMF class. We can use that to do all the tough work here. I’ll be using the ORL images dataset for this. This is a classic greyscale faces dataset that’s been used in computer vision for decades.

Here’s an example from the dataset:

source

Here’s the code to load all the images into a big numpy array:

    images = []
    for file in os.listdir('archive'):
        img = np.array(Image.open('archive/' + file))
        if len(img.shape) == 3: # some images come in rgb.
            img = img[:, :, 0] # not really desaturation.
        images.append(img.flatten())
    images = np.array(images)

Let’s make 20 latent faces:

    k = 20
    nmf_model = NMF(n_components=k, random_state=42)

    nmf_model.fit(images)

Now we can decompose the embeddings to see what the latent faces look like:

    images = []
    i = 0
    for image in nmf_model.components_:
        image = image.flatten()
        image.resize((80, 70))
        images.append(image)
        plt.figure()
        plt.savefig(f'imgs/{i}.png')
        i += 1

And here’s the cool generated face image:

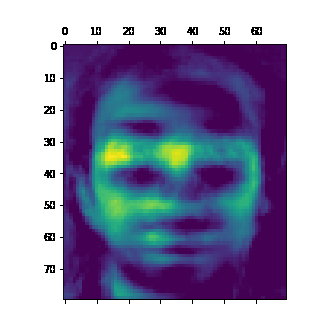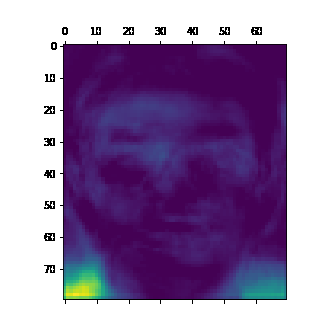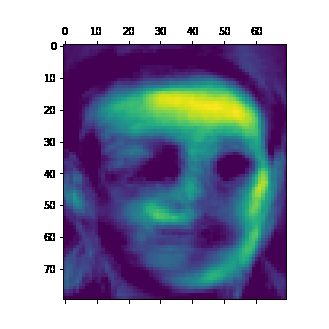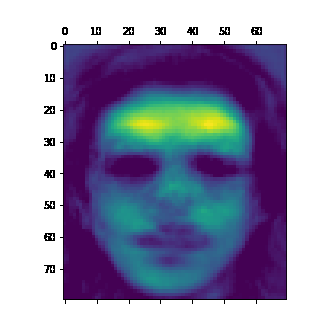
You can see that the faces aren’t entirely novel, and have characteristics of faces from the dataset, such as glasses. Overall it’s a pretty cool technique that shows an interesting aspect of NNMF and embeddings. I tend to work with embeddings a lot more with NLP in my work, so it’s great to have an eye-catching and visual demo of what the technique does.